二叉樹查找和刪除指定結點_ZenDei技術網路在線

二叉樹查找指定的節點前序查找的思路 1.先判斷當前節點的no是否等於要查找的 2.如果是相等，則返回當前節點 3.如果不等，則判斷當前節點的左子節點是否為空，如果不為空，則遞歸前序查找 4.如果左遞歸前序查找，找到節點，則返回，否繼續判斷，當前的節點的右子節點是否為空，如果不為空，則繼續向右遞歸前 ...

二叉樹查找指定的節點

前序查找的思路

1.先判斷當前節點的no是否等於要查找的

2.如果是相等，則返回當前節點

3.如果不等，則判斷當前節點的左子節點是否為空，如果不為空，則遞歸前序查找

4.如果左遞歸前序查找，找到節點，則返回，否繼續判斷，當前的節點的右子節點是否為空，如果不為空，則繼續向右遞歸前序查找。

中序查找思路

1.判斷當前節點的左子節點是否為空，如果不為空，則遞歸中序查找

2.如果找到，則返回，如果沒有找到，就和當前節點比較，如果是則返回當前節點，否則繼續進行右遞歸的中序查找

3.如果右遞歸中序查找，找到就返回，否則返回null

後序查找思路

1.判斷當前節點的左子節點是否為空，如果不為空，則遞歸後序查找

2.如果找到，就返回，如果沒有找到，就判斷當前節點的右子節點是否為空，如果不為空，則右遞歸進行後序查找，如果找到，就返回

3.就和當前節點進行比較，如果是則返回，否則返回null

要求

1.請編寫前序查找，中序查找和後序查找的方法。

2.並分別使用三種查找方式，查找 heroNO = 5 的節點

3.並分析各種查找方式，分別比較了多少次

代碼實現：

先創建HeroNode 結點

class HeroNode {
	private int no;
	private String name;
	private HeroNode left; //預設null
	private HeroNode right; //預設null
	public HeroNode(int no, String name) {
		this.no = no;
		this.name = name;
	}
	public int getNo() {
		return no;
	}
	public void setNo(int no) {
		this.no = no;
	}
	public String getName() {
		return name;
	}
	public void setName(String name) {
		this.name = name;
	}
	public HeroNode getLeft() {
		return left;
	}
	public void setLeft(HeroNode left) {
		this.left = left;
	}
	public HeroNode getRight() {
		return right;
	}
	public void setRight(HeroNode right) {
		this.right = right;
	}
	@Override
	public String toString() {
		return "HeroNode [no=" + no + ", name=" + name + "]";
	}
    //前序遍歷
	public void preOrder() {
		System.out.println(this); //先輸出父結點
		//遞歸向左子樹前序遍歷
		if(this.left != null) {
			this.left.preOrder();
		}
		//遞歸向右子樹前序遍歷
		if(this.right != null) {
			this.right.preOrder();
		}
	}
	//前序遍歷查找
	/**
	 * 
	 * @param no 查找no
	 * @return 如果找到就返回該Node ,如果沒有找到返回 null
	 */
	public HeroNode preOrderSearch(int no) {
		System.out.println("進入前序遍歷");
		//比較當前結點是不是
		if(this.no == no) {
			return this;
		}
		//1.則判斷當前結點的左子節點是否為空，如果不為空，則遞歸前序查找
		//2.如果左遞歸前序查找，找到結點，則返回
		HeroNode resNode = null;
		if(this.left != null) {
			resNode = this.left.preOrderSearch(no);
		}
		if(resNode != null) {//說明我們左子樹找到
			return resNode;
		}
		//1.左遞歸前序查找，找到結點，則返回，否繼續判斷，
		//2.當前的結點的右子節點是否為空，如果不空，則繼續向右遞歸前序查找
		if(this.right != null) {
			resNode = this.right.preOrderSearch(no);
		}
		return resNode;
	}
	
	//中序遍歷查找
	public HeroNode infixOrderSearch(int no) {
		//判斷當前結點的左子節點是否為空，如果不為空，則遞歸中序查找
		HeroNode resNode = null;
		if(this.left != null) {
			resNode = this.left.infixOrderSearch(no);
		}
		if(resNode != null) {
			return resNode;
		}
		System.out.println("進入中序查找");
		//如果找到，則返回，如果沒有找到，就和當前結點比較，如果是則返回當前結點
		if(this.no == no) {
			return this;
		}
		//否則繼續進行右遞歸的中序查找
		if(this.right != null) {
			resNode = this.right.infixOrderSearch(no);
		}
		return resNode;
		
	}
	
	//後序遍歷查找
	public HeroNode postOrderSearch(int no) {
		
		//判斷當前結點的左子節點是否為空，如果不為空，則遞歸後序查找
		HeroNode resNode = null;
		if(this.left != null) {
			resNode = this.left.postOrderSearch(no);
		}
		if(resNode != null) {//說明在左子樹找到
			return resNode;
		}
		
		//如果左子樹沒有找到，則向右子樹遞歸進行後序遍歷查找
		if(this.right != null) {
			resNode = this.right.postOrderSearch(no);
		}
		if(resNode != null) {
			return resNode;
		}
		System.out.println("進入後序查找");
		//如果左右子樹都沒有找到，就比較當前結點是不是
		if(this.no == no) {
			return this;
		}
		return resNode;
	}
	
}

定義BinaryTree 二叉樹

class BinaryTree {
	private HeroNode root;

	public void setRoot(HeroNode root) {
		this.root = root;
	}
	
	//前序遍歷查找
	public HeroNode preOrderSearch(int no) {
		if(root != null) {
			return root.preOrderSearch(no);
		} else {
			return null;
		}
	}
	//中序遍歷查找
	public HeroNode infixOrderSearch(int no) {
		if(root != null) {
			return root.infixOrderSearch(no);
		}else {
			return null;
		}
	}
	//後序遍歷查找
	public HeroNode postOrderSearch(int no) {
		if(root != null) {
			return this.root.postOrderSearch(no);
		}else {
			return null;
		}
	}
}

測試：

public class BinaryTreeDemo {

	public static void main(String[] args) {
		//先需要創建一顆二叉樹
		BinaryTree binaryTree = new BinaryTree();
		//創建需要的結點
		HeroNode root = new HeroNode(1, "宋江");
		HeroNode node2 = new HeroNode(2, "吳用");
		HeroNode node3 = new HeroNode(3, "盧俊義");
		HeroNode node4 = new HeroNode(4, "林沖");
		HeroNode node5 = new HeroNode(5, "關勝");
		
		//說明，我們先手動創建該二叉樹，後面我們學習遞歸的方式創建二叉樹
		root.setLeft(node2);
		root.setRight(node3);
		node3.setRight(node4);
		node3.setLeft(node5);
		binaryTree.setRoot(root);
		
		// 前序遍歷
		// 前序遍歷的次數 ：4
		System.out.println("前序遍歷方式~~~");
		HeroNode resNode = binaryTree.preOrderSearch(5);
		if (resNode != null) {
			System.out.printf("找到了，信息為 no=%d name=%s", resNode.getNo(), resNode.getName());
		} else {
			System.out.printf("沒有找到 no = %d 的英雄", 5);
		}
		
		/**
			// 中序遍歷查找
			// 中序遍歷3次
			System.out.println("中序遍歷方式~~~");
			HeroNode resNode = binaryTree.infixOrderSearch(5);
			if (resNode != null) {
				System.out.printf("找到了，信息為 no=%d name=%s", resNode.getNo(), resNode.getName());
			} else {
				System.out.printf("沒有找到 no = %d 的英雄", 5);
			}
		*/
		/**
			// 後序遍歷查找
			// 後序遍歷查找的次數 2次
			System.out.println("後序遍歷方式~~~");
			HeroNode resNode = binaryTree.postOrderSearch(5);
			if (resNode != null) {
				System.out.printf("找到了，信息為 no=%d name=%s", resNode.getNo(), resNode.getName());
			} else {
				System.out.printf("沒有找到 no = %d 的英雄", 5);
			}
		*/
		
	}

}

運行結果如圖：

前序遍歷：

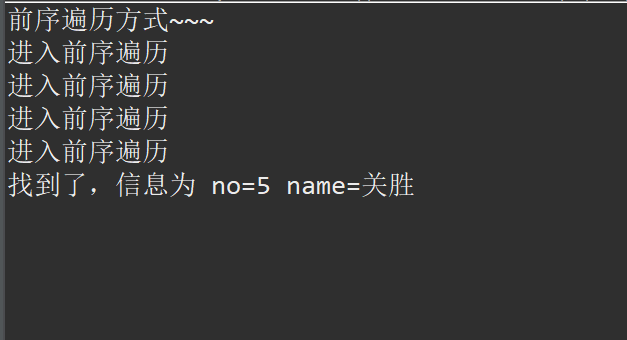
中序遍歷：

後序遍歷：

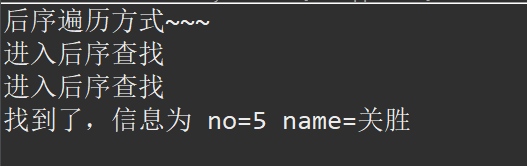
二叉樹刪除指定的節點

要求

1.如果刪除的節點是葉子節點，則刪除該節點

2.如果刪除的節點是非葉子節點，則刪除該子樹.

3.測試，刪除掉 5 號葉子節點

思路：

1.考慮如果樹是空樹root,如果只有一個root節點，則等價將二叉樹置空

2.因為我們的二叉樹是單向的，所以我們是判斷當前節點的子節點是否是需要刪除節點，而不能去判斷當前這個節點是不是需要刪除節點。

3.如果當前節點的左子節點不為空，並且左子節點就是要刪除節點，就將this.left=null;

並且就返回（結束遞歸刪除）

4.如果當前節點的右子節點不為空，並且右子節點就是要刪除節點，就將this.right=null;

並且就返回（結束遞歸刪除）

5.如果3，4步沒有刪除節點，那麼我們就需要向左子樹進行遞歸刪除

6.如果第5步也沒有刪除節點，則應當向右子樹進行遞歸刪除。

代碼實現：

//HeroNode 類增加方法

//遞歸刪除結點
	//1.如果刪除的節點是葉子節點，則刪除該節點
	//2.如果刪除的節點是非葉子節點，則刪除該子樹
	public void delNode(int no) {
		
		//思路
		/*
		 * 	1. 因為我們的二叉樹是單向的，所以我們是判斷當前結點的子結點是否需要刪除結點，而不能去判斷當前這個結點是不是需要刪除結點.
			2. 如果當前結點的左子結點不為空，並且左子結點 就是要刪除結點，就將this.left = null; 並且就返回(結束遞歸刪除)
			3. 如果當前結點的右子結點不為空，並且右子結點 就是要刪除結點，就將this.right= null ;並且就返回(結束遞歸刪除)
			4. 如果第2和第3步沒有刪除結點，那麼我們就需要向左子樹進行遞歸刪除
			5.  如果第4步也沒有刪除結點，則應當向右子樹進行遞歸刪除.

		 */
		//2. 如果當前結點的左子結點不為空，並且左子結點 就是要刪除結點，就將this.left = null; 並且就返回(結束遞歸刪除)
		if(this.left != null && this.left.no == no) {
			this.left = null;
			return;
		}
		//3.如果當前結點的右子結點不為空，並且右子結點 就是要刪除結點，就將this.right= null ;並且就返回(結束遞歸刪除)
		if(this.right != null && this.right.no == no) {
			this.right = null;
			return;
		}
		//4.我們就需要向左子樹進行遞歸刪除
		if(this.left != null) {
			this.left.delNode(no);
		}
		//5.則應當向右子樹進行遞歸刪除
		if(this.right != null) {
			this.right.delNode(no);
		}
	}

//在 BinaryTree 類增加方法

//刪除結點
	public void delNode(int no) {
		if(root != null) {
			//如果只有一個root結點, 這裡立即判斷root是不是就是要刪除結點
			if(root.getNo() == no) {
				root = null;
			} else {
				//遞歸刪除
				root.delNode(no);
			}
		}else{
			System.out.println("空樹，不能刪除~");
		}
	}

//在 BinaryTreeDemo 類增加測試代碼：

//測試一把刪除結點
		System.out.println("刪除前,前序遍歷");
		binaryTree.preOrder(); //  1,2,3,5,4
		binaryTree.delNode(5);
		//binaryTree.delNode(3);
		System.out.println("刪除後，前序遍歷");
		binaryTree.preOrder(); // 1,2,3,4

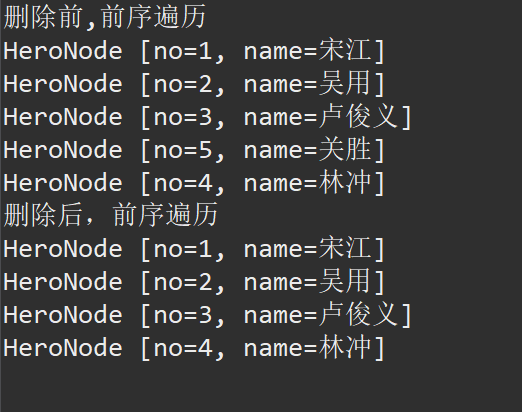
代碼運行如圖：

這篇博客是我在B站看韓順平老師數據結構和演算法的課時的筆記，記錄一下，防止忘記，也希望能幫助各位朋友。